Constraint satisfaction problems
Constrain Satisfaction Problems (CSPs)
- CSPs are a subset of search problems in general
- State defined by variables , with values from a domain
- “Goal test” is set of constraints specifying allowable combinations of values for subsets of variables
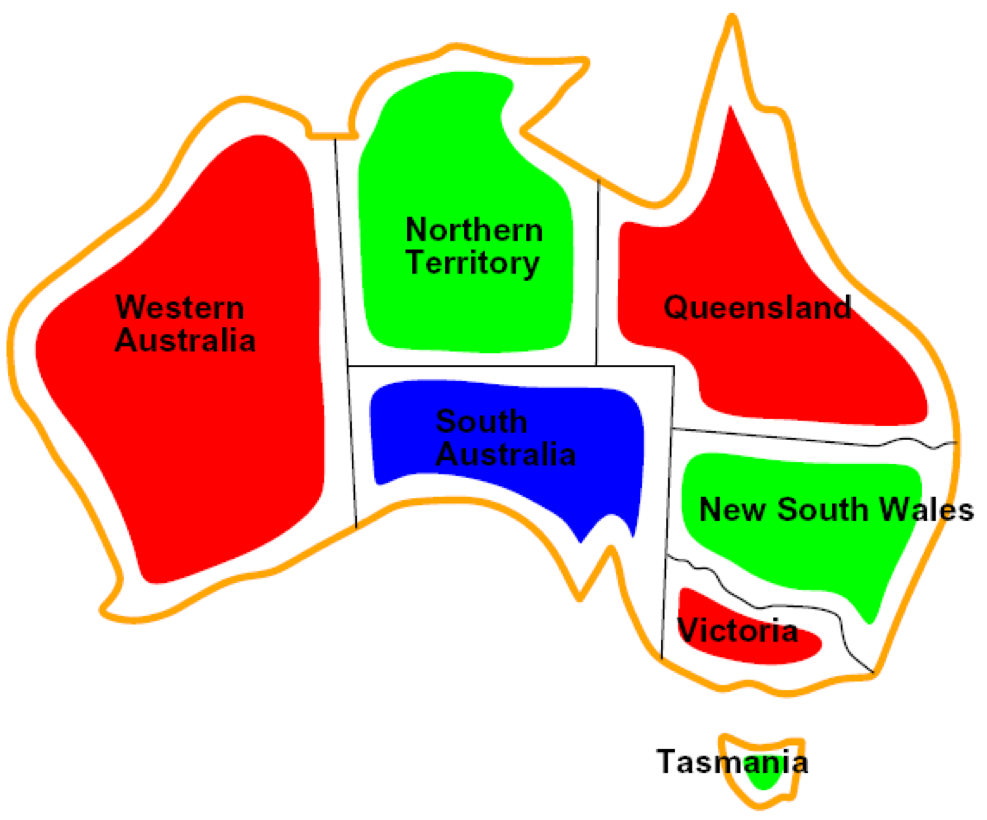
Example: Map Coloring (for Australia)
- Variables: WA, NT, Q, NSW, V, SA, T
- Domain:
- Constraints: adjacent regions must not have same color, can be encoded implicitly or explicitly
- Implicit could be region colors , whereas explicit would be explicitly stating what’s allowed
- Solutions are assignments of elements in the domain to the variables such that all constraints are satisfied. In this example, a solution might be something like
Constraint Graphs
- Binary CSP: constraints relate at most two variables; variables represented as nodes, edges between nodes indicate a constraint involved those variables
Varieties of CSPs
- Discrete variables
- Finite domains like boolean CSPs, variables take on one value from a finite set
- Infinite domains like integers, strings
- Continuous variables
- Variables can take on continuous values like times
Backtracking Search
- Imagine solving a constraint graph using DFS or BFS, where we start with an empty assignment and a successor function assigns some value to an unassigned variable. DFS, for example, will naively make its way through all variables assigning values randomly until it hits a leaf, steps back, and tries the next assignment that leaf, and so on. This will continue all the way back up the tree (path through the constraint graph) until some valid combination of assignments are made. This is often incredibly bad. What to do?
- Attempt to augment depth search by identifying early on that we’re in a bad state, as opposed to wasting time exploring the entire state only to make the same conclusion. This is called backtracking search, and is the basic uninformed algorithm for solving CSPs.
- Idea 1: Approach one variable at a time i.e. only considering or fixing assignments to individual variables at each time step
- Idea 2: Check constraints dynamically on the go
Backtracking search is depth-first search with these two ideas implemented. Can implement backtracking with a few things in mind:
- Ordering: In what order should we select variables to be assigned, and in what order should its possible values be tried?
- Filtering: Can failure be detected early?
- Structure: How to exploit problem structure?
Filtering
Filtering keeps track of domains for variables yet to be assigned, and values are crossed off if they are deemed bad.
Forward Checking
Forward checking is a filtering method that removes values from a variable’s domain when they would violate a constraint if added to the current assignment. Note this doesn’t feel all that much different from vanilla backtracking search locally, but filtering applies globally. That is, without forward checking, we would only begin to backtrack when there is no valid value to assign the next variable, whereas with filtering we begin backtracking as soon as any variable has no remaining valid domain values. Essentially this is just a slight modification that allows us to detect bad assignments earlier on.
Constraint Propagation
Forward checking propagates information from assigned values to unassigned ones, but does not always detect when there are problems across variable domains. For example, in the map coloring example above, forward checking will begin backtracking when some variable has an empty domain. However, it will not necessarily backtrack when two neighboring states both have the same, single color left in their domains. Clearly they can’t both be assigned that color, but forward checking will not detect that this is a problem because it does not detect issues across constraints.
Constraint propagation address this problem by enforcing consistency of arcs. An arc is consistent if and only if for every in the tail there is some in the head which could be assigned without violating a constraint. This ensures that, whenever we make an assignment to a variable, that information propagates through the rest of the graph and updates domains that are affected. For values that break this consistency, we delete them from the tail. - Note that when values are removed from the domain of a variable , we need to recheck the variables who have an arc head pointing to the variable
-consistency
The idea of increasing levels of consistency - 1-consistency (node consistency): each node’s domain has a value meeting its unary constraints - 2-consistency (arc consistency): each pair of nodes have consistent assignments between each other - 1-consistency (node consistency): for each group of nodes, any consistent assignment to of them can be extended to the
Structure
- Independent subproblems can be identified as connected components in the constraint graph
Ordering: Minimum Remaining Values
- Heuristic for ordering the variables to which we assign values as we process search i.e. which variables to pick assignments for first
- The idea is to choose from the set of variables currently with the fewest values remaining in their domain. (Note: this is exactly what WFC does when “collapsing states”; the direction of minimal entropy is followed immediately, prioritizing those variables whose state we know the most about. Those variables with a greater number of remaining values in their domains have a greater uncertainty as to their final state, and hence we process them after the more certain variables.)
Ordering: Least Constraining Value
- Heuristic on order of values with variables (i.e. given that a variable has already been chosen) that chooses the least constraining value
- This leaves the largest possible number of remaining states for other variables, giving us greater flexibility as we continue to searchA
Iterative Algorithms
Start with a complete assignment where all variables have assigned values, and iteratively fix problems. - Pick a variable with conflicts at random - Reassign the value to that variable that violates the fewest constraints
Turns out this strategy is very effective for virtually any random CSP except for those having a critical ratio of number of constraints to number of variables. That is, with a large number of constraints and few variables (or vice versa), the CSP is quite easy to solve with an iterative reassignment approach. But those with critical ratio of variables to constraints (no explicitly ratio is given) turn out to take a ton of time with limited success.
CSP Summary
- CSPs are subset of search problems, where states are partial assignments, and goals are assignments without constrain conflicts
- Basic approach to solving CSPs is backtracking search, with common speedups using ordering, filtering, and exploiting problem structure
- Iterative algorithms with min-conflicts is often an effective approach as well
Local Search
- Tree search keeps track of unexplored values on the fringe to ensure completeness, but can be slow and take extra memory
- Local search improves a single option until it can’t be made any better (no fringe tracking needed)
Hill Climbing
Start somewhere and move to the best neighboring state. Continue this until there are no neighbors better than current position. Not complete (may never reach a local optima) or optimal (may get stuck in local max), but often useful
Simulated Annealing
Hill climbing but smarter: continuously decrease a “temperature” parameter which controls the probability of taking a downward step. This helps to bounce out of local maxima early on, and ultimately leads to convergence if the temperature is decreased slowly enough
Genetic Algorithms
Know these for now