Learning theory
Target Function
The target function can be expressed as “noisy”, or as a distribution, without loss of generalization, since a distribution can be defined such that 100% of the time it is one particular value. Modeling a target distribution allows us to incorporate inherit stochasticity into our model that simply cannot be accounted for (i.e. when the exact same input leads to differing outputs). This target is represented by the conditional density
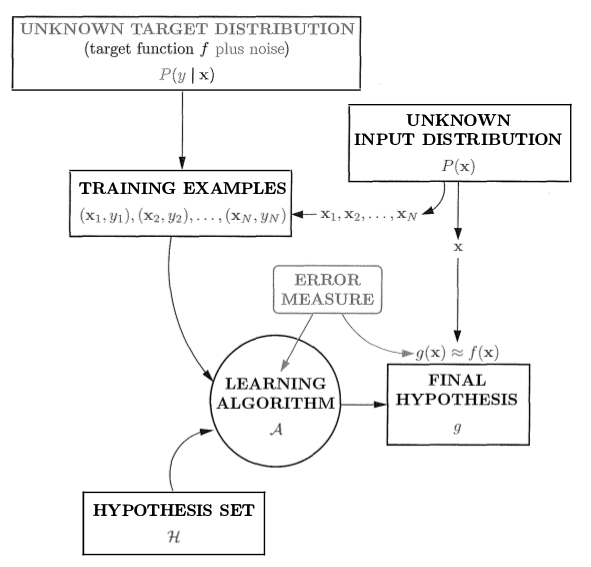
Note that in a formulation like this, the unknown input distribution quantifies the relative importance of the samples . The training examples are assumed to have been sampled from the input space according to , and its important that we make the same assumption when testing the model outside of the training data. Firstly, in an example where we have a number of factors about a person and would like to decide whether to issue them a loan, we might have the exact same inputs lead to different outputs in our training data (or outside of it). So the target function, which is a function defined on the the input space (ie not on all possible factors, explaining prior confusion regarding the deterministic nature of the target), cannot be deterministic and must be modeled with the idea of adding noise (ie as a distribution ). Additionally, to another point, suppose one of the attributes in the input space is current income. Although in the input space this value can be arbitrarily large, the vast majority of samples won’t exceed a particular value (say 100k). So it is very much the case that the training samples (as well as instances in the real world, outside of the training set!) come from this unknown distribution defined on the input space. And this matters because it allows us to train and evaluate our model in the same context; it wouldn’t be fair, nor would it be useful, say, to train on the training set and then evaluate on the entire input space with equal weight to all points.
Hash out
- Q: I get why it makes sense to model the target as a distribution. It is often the case that we can have the exact some features lead to a different class label. This is obviously a probabilistic setting, since we can’t determine exactly the output from the input. But, is it assumed that there is a deterministic function that can? If we have enough features (ie all of them) about a real world scenario, we should be able to deterministically model the target, right? A: Yes, this is correct. If you knew everything there is to know, sure (there is no longer any uncertainty; all sources of uncertainty have been quantified). But this, even in theory, is pretty much useless. The theory refers to the same data space that’s being modeled, and represents the optimal distribution on the space underlying the experiment.
Example
Estimating the bias of a coin: There is a true bias of the coin, unknown to us. Then there is our model of the coin’s bias, perhaps based on previous observations and some on prior beliefs (if we’re a Bayesian). This problem formulation is simply concerned with modeling the bias of the coin, or the data generating distribution (where the data are outcomes of coin flips). In other words, the “target” is the correct value of the parameter, or the true distribution over the data. If we wanted to “predict” the side of the coin that will come up on the next flip, we can simply look at the expected value (and other metrics) of to make a statement about our beliefs. Note that there is not exactly a target value to predict based on input, though; we just have observations of coins flips, or the data . This is an example of a generative modeling scenario.
Now consider a more standard supervised ML scenario. You have some input output pairs , and you want to learn about the correlation between the two (i.e. what can tell you about ). Let be a series of attributes about a person who was given a loan from a bank (credit score, last year’s income, etc) and let y be whether or not the person defaulted on the loan. The goal of this task is to predict whether a person will default on a loan, given the information we have about them. This problem formulation is not concerned (directly) with modeling the distribution of people given loans (that is, ) as before. If it were, this would be the equivalent of wanting to “predict” the attributes of the next person we will see come in for a loan, a generative task. Instead the goal is to learn about the relation between the two variables by modeling the conditional distribution . This is a distribution over the possible outputs (yes or no in this case), given the particular attributes about the person who wants the loan. This is a discriminative modeling scenario.
Hypothesis space
Hoeffding bound
VC dimension
Bias and variance
Overfitting and underfitting
Regularization: regularization is bayesian, i.e. a prior over the parameters. When stated in terms of a loss function, the model must make a tradeoff between adhering to the prior structural assumptions of the regularization function and fitting the data with its massive capacity.